树是一种较为复杂的数据结构，人们这样定义它：“由一个或多个(n>=0)节点组成的有限集合T，有且只有一个’根’节点（root），当n>1时，其余的结点分为m(m≥0)个互不相交的有限集合T1,T2，…，Tm。每个集合本身又是棵树，被称作这个根的子树 。”我们首先来看一下我们对其逻辑结构的表示图：
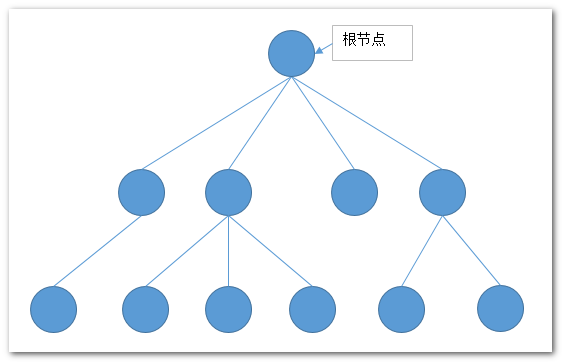相对于逻辑结构，其物理储存结构也与我们之前学习过的一些基础结构差不多，要么是一块连续的空间储存，要么是链的方式储存。下面我们总结一下树的特性：
- 树是多个互不相交的集合
- 树是可以为空的
- 树是递归定义的
【树的若干术语】
**根：**既根节点（没有前驱）上图中A节点 **叶子：**既终端节点（没有后继）上图中K L M节点 **森林：**指m棵不相交的树的集合（例如删除A后的子树个数） **有序树：**结点各子树从左至右有序，不能互换（左为第一） **无序树：**结点各子树可互换位置。 **双亲：**即上层的那个结点(直接前驱) parent **孩子：**即下层结点的子树 (直接后继) child **兄弟：**同一双亲下的同层结点（孩子之间互称兄弟）sibling **堂兄弟：**即双亲位于同一层的结点（但并非同一双亲）cousin **祖先：**即从根到该结点所经分支的所有结点 **子孙：**即该结点下层子树中的任一结点 **节点：**即树的数据元素 **节点的度：**结点挂接的子树数（有几个直接后继就是几度，亦称“次数”）从根到该结点的层数（根结点算第一层） **节点的层次：**从根到该结点的层数（根结点算第一层） **终端节点：**即度为0的结点，即叶子 **分支节点：**除树根以外的结点（也称为内部结点） **树的度：**所有结点度中的最大值（Max{各结点的度}） **树的深度：**指所有结点中最大的层数（Max{各结点的层次}）